Tìm tất cả các giá trị thực của tham số m  để đường thẳng y= - mx lần lượt cắt đồ thị của hàm số y= x³- 3x²-m+ 2 tại ba điểm phân biệt theo thứ tự A; B; C  sao cho AB = BC.

Cho hàm số y=x⁴-(3m+4) x²+ m² có đồ thị là C. Có mấy giá trị nguyên của m để đồ thị C cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.

Cho phương trình x³- 3x²+ 1- m=0  (1) . Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa m ãn x₁< 1< x₂<x₃  khi

Cho đồ thị C: y= 2x³-3x²-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k  để  C cắt d tại ba điểm phân biệt là

Với những giá trị nào của tham số m thì (C) : y= x³- 3( m+ 1) x²+ 2( m ²+ 4m+1 ) x-4m( m+1 )  cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?

Hỏi phương trình 3x²- 6x+ ln( x+1)³+1=0  có bao nhiêu nghiệm phân biệt?

Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số $y=\frac{1}{3}{x}^3-m{x}^2+(m^2-1)x$  có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y= 5x- 9 . Tính tổng tất cả các phần tử của S.

Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số $y=x^4-2m{x}^2$  có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.

Cho hàm số $y=\frac{2x+1}{x+1}$  có đồ thị C  và d: y= x+ m. Giá trị của tham số m để d cắt C tại hai điểm phân biệt A; B sao cho tiếp tuyến tại  A  và B  song song với nhau.

Tìm tất cả các giá trị thực của tham số m  để đường thẳng y= - mx lần lượt cắt đồ thị của hàm số y= x³- 3x²-m+ 2 tại ba điểm phân biệt theo thứ tự A; B; C  sao cho AB = BC.

Cho hàm số y= x³- 3x²-m- 1 có đồ thị ( C) . Giá trị của tham số m  để đồ thị C  cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số $y=x^3+mx-\frac{1}{5x^5}$  đồng biến  với x> 0?

Gọi S  là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số  $y=\left|x^2-3x+m\right|$ trên đoạn [ 0; 2]  bằng 3. Số phần tử của  S là

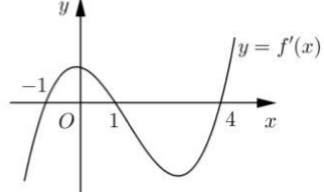
Cho hàm số y = f(x).Hàm số y= f’(x) có đồ thị như hình bên. Hỏi hàm số y= f(2-x)  đồng biến trên khoảng:

Cho hàm số  $y=\frac{-x+2}{x-1}$ có đồ thị (C)  và điểm A( a; 1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Hỏi trong tập S có bao nhiêu giá trị nguyên

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số  $y=\left|3x^4-4x^3-12x^2+m\right|$ có 7 điểm cực trị?

Cho hàm số  y= x⁴- (2m-1) x²+2m có đồ thị (C) . Có tất cả bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y= 2  cắt đồ thị (C)  tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là

Cho hàm số y= x³- 3mx²+ 3( m+1) x+1   (1)  với m là tham số. Gọi (C)  là đồ thị hàm số (1) và K là điểm thuộc (C)   có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m  để tiếp tuyến của ( C)  tại điểm K  song song với đường thẳng d: 3x+ y= 0  là

Cho hàm số y= x³- x²+ x + 1  có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y)  của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2)  .  Khi đó x+ y=?

Cho hàm số y= x⁴- 2mx²+m   (1) với m là tham số thực. Gọi (C) là đồ thị hàm số (1); d là tiếp tuyến của (C) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B( ¾; 1)  đến đường thẳng d đạt giá trị lớn nhất?

Cho hàm số $y=\frac{2x+3}{x+1}$  có đồ thị là (C) . Có bao nhiêu tiếp tuyến của đồ thị (C)  tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng d₁: 3x+ 4y-2=0  bằng 2.