HỌC VIỆN HOÀNG GIA
200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P5)
Đề thi đã ghi nhận 16269 lượt thi, với 20 câu hỏi được thiết kế nhằm đánh giá toàn diện kiến thức môn Toán Lớp 12 của học sinh. Thời gian làm bài là 20 phút. Đề thi nhận được hơn 787 lượt đánh giá tích cực từ những học sinh đã tham gia làm bài
LÀM BÀI THI
Cho hàm số y=x4-(3m+4) x2+ m2 có đồ thị là C. Có mấy giá trị nguyên của m để đồ thị C cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.
Phương trình hoành độ giao điểm: x4-(3m+4) x2+ m2 = 0 ( 1)
Đặt t= x2, phương trình trở thành: t2-(3m+4)t+ m2 = 0 ( 2)
C cắt trục hoành tại bốn điểm phân biệt khi và chỉ khi ( 1) có bốn nghiệm phân biệt
Khi đó ( 2) có hai nghiệm dương phân biệt
+ Khi đó phương trình *(2) có hai nghiệm 0<t1< t2. Suy ra phương trình (1) có bốn nghiệm phân biệt là . Bốn nghiệm x1; x2; x3; x4 lập thành cấp số cộng
Theo định lý Viet ta có
Từ (3) và (4) ta suy ra được
Thay (6) vào (5) ta được
Vậy giá trị m cần tìm làm =12; m= -12/ 19
Chọn B.
Cho phương trình x3- 3x2+ 1- m=0 (1) . Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa m ãn x1< 1< x2<x3 khi
Ta có x3- 3x2+ 1- m=0 là phương trình hoành độ giao điểm giữa hai đồ thị hàm số
y= x3- 3x2+ 1 và y= m (là đường thẳng song song hoặc trùng với Ox).
+Xét y= x3- 3x2+ 1 .
Đạo hàm y’ = 3x2- 6x
Ta có y’=03x2- 6x=0
Khi x= 1 thì y= -1
Dựa vào đồ thị, yêu cầu bài toán khi và chỉ khi -3< m< -1 .
Chọn C.
Cho đồ thị C: y= 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là
+ Phương trình đường thẳng d có dang d: y= kx-1 .
Phương trình hoành độ giao điểm của đồ thị C và đường thẳng d:
+ Để C cắt d tại ba điểm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt khác 0
Vậy chọn
Chọn B.
Với những giá trị nào của tham số m thì (C) : y= x3- 3( m+ 1) x2+ 2( m 2+ 4m+1 ) x-4m( m+1 ) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?
+ Phương trình hoành độ giao điểm của đồ thị C và trục Ox:
x3- 3(m + 1) x2+ 2(m 2 + 4m + 1)x - 4m(m + 1)= 0
hay ( x- 2) [x2-( 3m+ 1) x+ 2m2+ 2m] =0
Yêu cầu bài toán
Vậy ½< m và m≠ 1.
Chọn A.
Hỏi phương trình 3x2- 6x+ ln( x+1)3+1=0 có bao nhiêu nghiệm phân biệt?
Điều kiện: x> -1
Ta có: 3x2- 6x+ ln( x+1)3+1=0 hay 3x2- 6x+ 3ln( x+1)+1=0
f(x)=3x2- 6x+ 3ln(x + 1) + 1
Đạo hàm f’ (x) = 0 khi và chỉ khi (2x- 2)(x+ 1) +1=0
Từ đây, ta có bảng biến thiên của f(x):
Nhìn vào bảng biến thiên ta sẽ có phương trình đã cho có 3 nghiệm phân biệt.
Chọn C.
Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y= 5x- 9 . Tính tổng tất cả các phần tử của S.
+ Ta có đạo hàm y’ = x2- 2mx+ (m2-1).
Phương trình y’ =0 có
+ Không mất tính tổng quát, giả sử
A, B nằm khác phía khi và chỉ khi x1. x2< 0 hay ( m-1) (m+ 1) < 0
Suy ra -1< m< 1
A, B cách đều đường thẳng y= 5x-9 suy ra trung điểm I của AB nằm trên đường thẳng đó.
Khi đó ta có:
Ta có:
Suy ra
Chọn A
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
+ Điều kiện để hàm số có 3 cực trị là m> 0
+ Các điểm cực trị tạo thành tam giác cân có đáy bằng 2√m, đường cao bằng m2. (như hình bên )
Ta được
+ Để tam giác có diện tích nhỏ hơn 1 thì
Chọn D.
Cho hàm số có đồ thị C và d: y= x+ m. Giá trị của tham số m để d cắt C tại hai điểm phân biệt A; B sao cho tiếp tuyến tại A và B song song với nhau.
+ Phương trình hoành độ giao điểm của đồ thị C và đường thẳng d
+ Khi đó d cắt C tại hai điểm phân biệt A; B khi và chi khi phương trình (1) có hai nghiệm phân biệt khác -1
Khi đó ta lại có A( x1 ; x1+m) ; B( x2 ; x2+ m) ;
nên
và
Từ đây ta có
Vậy m= 0 hoặc m= 6.
Chọn D.
Tìm tất cả các giá trị thực của tham số m để đường thẳng y= - mx lần lượt cắt đồ thị của hàm số y= x3- 3x2-m+ 2 tại ba điểm phân biệt theo thứ tự A; B; C sao cho AB = BC.
+ Hoành độ giao điểm là nghiệm của phương trình
x3- 3x2-m+ 2= -mx hay ( x-1) ( x2-2x+ m-2) =0
Hay x=1; x2-2x+m-2=0
+ Đặt nghiệm x2= 1; từ giải thiết bài toán trở thành tìm m để phương trình có 3 nghiệm lập thành cấp số cộng. Khi đó phương trình : x2-2x+m-2 = 0 phải có 2 nghiệm phân biệt (vì theo hệ thức Viet ta có: x1+ x3= 2= 2x2 ).
Vậy khi đó ta cần ∆’ > 0( để phương trình có 2 nghiệm phân biệt )
∆’=1-(m-2)>0
Chọn C.
Cho hàm số y= x3- 3x2-m- 1 có đồ thị ( C) . Giá trị của tham số m để đồ thị C cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
+ Đồ thị C cắt trục hoành tại điểm phân biệt tạo thành cấp số cộng khi và chỉ khi phương trình x3- 3x2- 1=m có ba nghiệm phân biệt lập thành cấp cố cộng.
+ Suy ra đường thẳng y= m đi qua điểm uốn của đồ thị y= x3- 3x2- 1
(do đồ thị (C) nhận điểm uốn làm tâm đối xứng).
+ Mà điểm uốn của đồ thị đã cho là I( 1 ; -3)
( hoành độ điểm uốn là nghiệm phương trình y’’= 0 hay y’’= 6x-6=0 do đó x= 1 ; y= -3)
Suy ra m= -3.
Chọn C.
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số đồng biến với x> 0?
+ Hàm số xác định và liên tục với mọi x> 0.
Ta có
+ Hàm số đồng biến trên khoảng (0; +∞) khi và chỉ khi với mọi x> 0.
Bảng biến thiên
Suy ra maxg( x) = g(1) = -4 và do đó để hàm số đã cho đồng biến t với x > 0 thì m ≥ -4
Mà m nguyên âm nên .
Chọn A.
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số trên đoạn [ 0; 2] bằng 3. Số phần tử của S là
+ Xét hàm số f(x) = x3-3x+ m là hàm số liên tục trên đoạn [0; 2] .
Ta có đạo hàm f’ (x) = 3x2- 3 và f’ (x) = 0 khi x= 1 ( nhận ) hoặc x= -1( loại)
+ Suy ra GTLN và GTNN của f(x) thuộc { f(0); f(1) ; f(2) }={m;m-2; m+2}.
+ Xét hàm số trên đoạn [0; 2 ] ta được giá trị lớn nhất của y là
TH1: m= 3 thì max {1;3;5}= 5 ( loại )
TH2:
+ Với m= -1. Ta có max {1; 3}= 3 (nhận).
+Với m= 5. Ta có max { 3;5;7}= 7 (loại).
TH3:
+ Với m= 1. Ta có max {1; 3}= 3 (nhận).
+ Với m= -5. Ta có max {3;5;7}= 7 (loại).
Do đó m= -1 hoặc m= 1
Vậy tập hợp S có 2 phần tử.
Chọn B.
Cho hàm số y = f(x).Hàm số y= f’(x) có đồ thị như hình bên. Hỏi hàm số y= f(2-x) đồng biến trên khoảng:
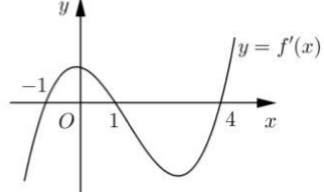
Ta có:( f( 2-x) )’= ( 2-x)’.f’(2-x) = -f’(2-x)
Hàm số đồng biến khi
Chọn D.
Cho hàm số có đồ thị (C) và điểm A( a; 1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Hỏi trong tập S có bao nhiêu giá trị nguyên
+ Phương trình đường thẳng d đi qua A và có hệ số góc k là: y= k( x-a) +1
+ Phương trình hoành độ giao điểm của d và (C) :
+ Với k = 0, ta có d: y= 1 là tiệm cận ngang đồ thị hàm số nên không thể tiếp xúc được.
+ Với k ≠ 0, d và (C) tiếp xúc nhau khi và chỉ khi (1) có nghiệm kép
Coi đây là phương trình bậc 2 ẩn k tham số a
+ Để qua A( a; 1) vẽ được đúng 1 tiếp tuyến thì phương trình 1 có đúng một nghiệm k ≠ 0.
*Xét 1-a= 0 hay a=1, ta có 4k+ k= 0 hạy k= -1 (thỏa mãn).
*Có f(0) = 4≠0 nên loại đi trường hợp có hai nghiệm trong đó có một nghiệm là k = 0.
*Còn lại là trường hợp ∆x= 0 có nghiệm kép khi
Vậy có 2 giá trị của a thỏa mãn đầu bài là a = 1 hoặc a = 3/2.
Chọn A.
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số có 7 điểm cực trị?
Xét hàm số y= 3x4- 4x3-12x2+m
Có
Ta có bảng biến thiên
Từ bảng biến thiên, để hàm số đã cho có 7 cực trị thì
Vì m nguyên nên các giá trị cần tìm của m là .
Chọn A.
Cho hàm số y= x4- (2m-1) x2+2m có đồ thị (C) . Có tất cả bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y= 2 cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là
+ Phương trình hoành độ giao điểm của (C) và đường thẳng d:
x4- (2m-1) x2+2m = 2 hay x4- (2m-1) x2+2m -2=0
Suy ra x2 = 1 hoặc x2 = 2m-2 (1)
+ Đường thẳng d cắt C tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương trình (1) có hai nghiệm phân biệt nhỏ hơn 3.
Do đó có 4 giá trị nguyên của m thỏa mãn đầu bài là: 2; 3; 4; 5.
Chọn D.
Cho hàm số y= x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y= 0 là
+Ta có đạo hàm y’ = 3x2- 6mx+ 3( m+ 1) .
Do K thuộc ( C) và có hoành độ bằng -1, suy ra K( -1; -6m-3)
y'(-1) = 9m + 6
Khi đó tiếp tuyến tại K có phương trình
∆: y = ( 9m+ 6) x+ 3m+ 3
Ta có: d:
Đường thẳng ∆ song song với đường thẳng d
Vậy không tồn tại m thỏa mãn đầu bài.
Chọn D.
Cho hàm số y= x3- x2+ x + 1 có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y) của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2) . Khi đó x+ y=?
Ta có: y' =
+ Đường thẳng ∆ đi qua điểm M( -1; -2) có hệ số góc k có dạng ∆: y= k( x+ 1) -2 .
+ ∆ là tiếp tuyến của (C ) khi và chỉ khi hệ sau có nghiệm:
+Thay (2) vào (1) ta được
x3- x2+ x+ 1= ( 3x2- 2x+1) (x+1) -2
Hay ( x+ 1)2.(x-1) =0
Suy ra x= -1 ( trùng với M nên loại ) hoặc x = 1
Với x = 1 thì y = 2. Vậy N(1; 2)
Chọn C.
Cho hàm số y= x4- 2mx2+m (1) với m là tham số thực. Gọi (C) là đồ thị hàm số (1); d là tiếp tuyến của (C) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B( ¾; 1) đến đường thẳng d đạt giá trị lớn nhất?
+ Do A thuộc (C ) nên A(1; 1-m) .
Đạo hàm y’ = 4x3 - 4mx nên y’ (1) = 4 - 4m .
+ Phương trình tiếp tuyến của (C) tại A là y - 1+ m = y’(1).(x-1),
Hay (4 - 4m).x - y - 3(1 - m) = 0.
+ Khi đó ,
Dấu ‘=’ xảy ra khi và chỉ khi khi m = 1.
Do đó khoảng cách từ B đến ∆ lớn nhất bằng 1 khi và chỉ khi m= 1.
Chọn B.
Cho hàm số có đồ thị là (C) . Có bao nhiêu tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng d1: 3x+ 4y-2=0 bằng 2.
+ Giả sử M( suy ra
+Ta có
Ta tìm được 4 điểm M suy ra có 4 tiếp tuyến.
Chọn C.
ĐỀ THI KHÁC TRONG BỘ ĐỀ THI
Bạn đang xem Đề số 1 thuộc bộ đề thi: 200 Trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao
Xem đề thi khác:
BỘ ĐỀ THI LIÊN QUAN
DANH SÁCH CÂU HỎI
Cho hàm số y=x4-(3m+4) x2+ m2 có đồ thị là C. Có mấy giá trị nguyên của m để đồ thị C cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.
Cho phương trình x3- 3x2+ 1- m=0 (1) . Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa m ãn x1< 1< x2<x3 khi
Cho đồ thị C: y= 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là
Với những giá trị nào của tham số m thì (C) : y= x3- 3( m+ 1) x2+ 2( m 2+ 4m+1 ) x-4m( m+1 ) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?
Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y= 5x- 9 . Tính tổng tất cả các phần tử của S.
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
Cho hàm số có đồ thị C và d: y= x+ m. Giá trị của tham số m để d cắt C tại hai điểm phân biệt A; B sao cho tiếp tuyến tại A và B song song với nhau.
Tìm tất cả các giá trị thực của tham số m để đường thẳng y= - mx lần lượt cắt đồ thị của hàm số y= x3- 3x2-m+ 2 tại ba điểm phân biệt theo thứ tự A; B; C sao cho AB = BC.
Cho hàm số y= x3- 3x2-m- 1 có đồ thị ( C) . Giá trị của tham số m để đồ thị C cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số trên đoạn [ 0; 2] bằng 3. Số phần tử của S là
Cho hàm số y = f(x).Hàm số y= f’(x) có đồ thị như hình bên. Hỏi hàm số y= f(2-x) đồng biến trên khoảng:

Cho hàm số có đồ thị (C) và điểm A( a; 1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Hỏi trong tập S có bao nhiêu giá trị nguyên
Cho hàm số y= x4- (2m-1) x2+2m có đồ thị (C) . Có tất cả bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y= 2 cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là
Cho hàm số y= x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y= 0 là
Cho hàm số y= x3- x2+ x + 1 có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y) của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2) . Khi đó x+ y=?